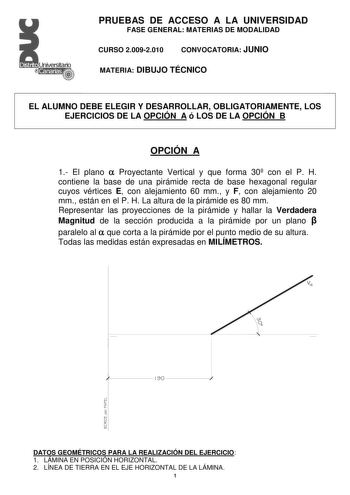
Examen de Matemáticas II de Canarias (PAU de 2010)

| Comunidad Autónoma | Islas Canarias |
|---|---|
| Asignatura | Matemáticas II |
| Convocatoria | Ordinaria de 2010 |
| Fase | Específica |
Temas mencionados new_releases
Matriz invertible
En matemáticas, en particular en álgebra lineal, una matriz cuadrada A de orden n se dice que es invertible, no singular, no degenerada o regular si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A−1, tal que, donde I'n es la matriz identidad de orden n y el producto utilizado es el producto de matrices usual.
Fuente: wikipedia.orgProducto vectorial
En matemáticas, el producto vectorial de Gibbs o producto cruz es una operación binaria entre dos vectores en un espacio tridimensional. El resultado es un vector perpendicular a los vectores que se multiplican, y por lo tanto normal al plano que los contiene. Debido a su capacidad de obtener un vector perpendicular a otros dos vectores, cuyo sentido varía de acuerdo al ángulo formado entre estos dos vectores, esta operación es aplicada con frecuencia para resolver problemas matemáticos, físicos o de ingeniería.
Fuente: wikipedia.orgTangente (geometría)
Tangente proviene del latín «tangens»=que toca. La tangente a una curva en un punto P, es una recta por P que toca a la curva solo en dicho punto llamado punto de tangencia; se puede decir que la tangente «forma un ángulo nulo» con la curva en la vecindad de dicho punto. Esta noción se puede generalizar, desde la recta tangente a un círculo o una curva, a «figuras tangentes» en dos dimensiones (es decir, figuras geométricas con un único punto de contacto, por ejemplo la circunferencia inscrita), hasta los espacios tangentes, en donde se clasifica el concepto de «tangencia» en más dimensiones.
Fuente: wikipedia.org